Project Overview
Thrust vectoring is the ability of an aircraft, rocket, or other vehicle to manipulate the direction of the thrust from its motor in order to control the attitude (angle) of the vehicle. It is used in rocketry it is the primary means of attitude control, as aerodynamic control surfaces are ineffective outside the atmosphere.

In a gimbaled thrust system, the exhaust nozzle of the rocket can be swiveled from side to side. As the nozzle is moved, the direction of the thrust is changed relative to the center of gravity of the rocket.
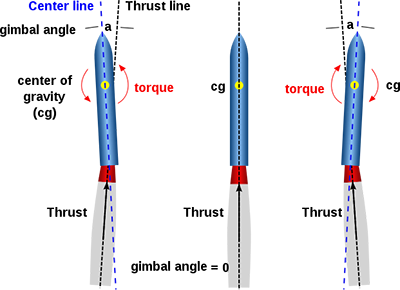
I started designing and building a model rocket with a gimbaled thrust system. Its controller should allow it to be stable and follow a pre-determined trajectory without the help of fins, reducing its aerodynamic drag.
Because of the complexity of this project, it will be divided into two articles:
- Part 1: Impulse - the rocket physics simulator
- Part 2: design, build & tests of the rocket [Work in progress]
The software
A rocket is a complex system and the impact of every variable must be known prior to the design process. The usage of a simulation software that computes the kinematics of the system solves this issue by allowing us to visualize these impacts, and tweak the variables to optimize the flight performances.
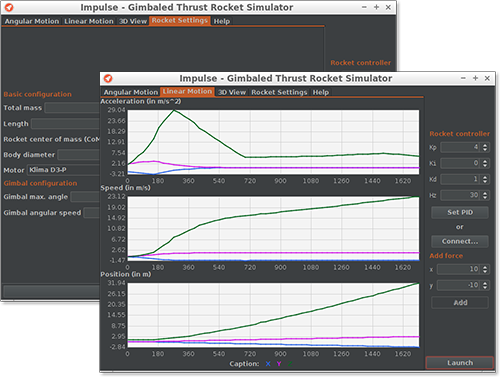
Impulse is a open-source and cross-platform simulator for gimbaled thrust rockets:
- It accurately simulates the physics and outputs real-time data;
- The simulated rocket is fully configurable;
- To visualize the kinetics of the rockets, there are several graphs (for linear and angular acceleration, speed and position) and a 3D view;
- A rocket controller board can be connected through a serial link.
The last point is a very useful feature of Impulse: it means that it is capable of testing the control algorithm on the rocket hardware.
Download and usage
To launch Impulse, execute the jar file. As an alternative, in can be executed from the command line with java -jar ImpulseRocketSimulator_v0.1.jar. Java Runtime Environnement 8 must be installed.
Download last release (GitHub)
The help tab in the software has all the required instructions in order to get started.
Technical Details
In this section, I will be doing a short technical overview of Impulse.
Physics engine
Impulse's engine is based on a physics model of the rocket I designed. It takes into account as many variables as possible to estimate the position and attitude of the rocket at any time: mass, repartition of mass, gimbal angle, motor thrust, etc.
This basic flow diagram represents the way the discrete computation can be implemented in computer code.
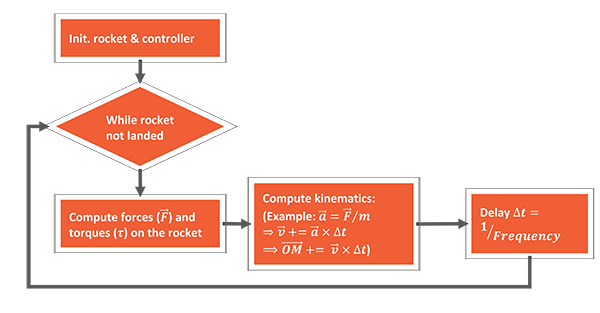
As the model advances to get more accurate, the physics engine is intended to evolve.
Frame of reference
The frame of reference is Galilean, with an (x,y,z) orthogonal coordinate centered on the launch point. To compute rotational motion, another coordinate system (x',y',z') centered on the thruster of the rocket is defined (see figure below).

The angle of the thruster relative to the rocket is (Gx, Gy, 0). We need to compute the projection of this vector in the coordinate system of the rocket. Geometrically:
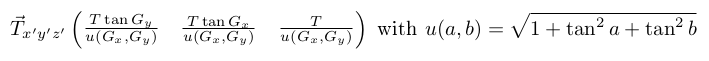
Similarly, the thrust along the long axis (z') of the rocket in the global frame of reference is:
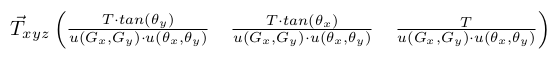
Dynamics of Translation Motion
For translation motion, we can simplify the problem by only considering the center of gravity of the rocket in our coordinate system (x,y,z). According to Newton's third law of dynamics:
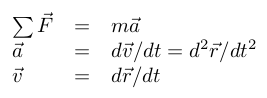
We consider 3 forces acting of the rocket:
- Weight
- Thrust
- Aerodynamic drag (currently ignored)
Hence:
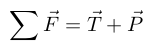
With:
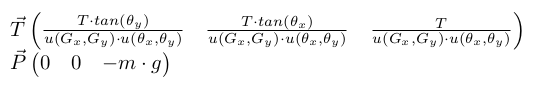
To be used on a computer, these equations must be discretized. This is simply a question of converting integrals to sums. Hence, the system used by the software is:
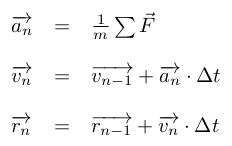
Dynamics of Rotational Motion
The equations for rotation are very similar to those for translation:
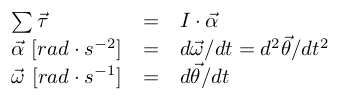
The rotation around the z axis is ignored. There are two torques acting on the x/y axes of the rocket:
- Thrust
- Aerodynamic drag (currently ignored)
Hence:
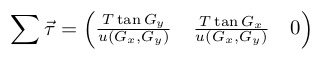
The I factor is the 3-dimensional moment of inertia, the quantity equivalent to mass for angular acceleration. It depends on the geometry of the rocket. Its mathematical expression is:
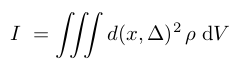
We assume that the rocket is axially symmetrical, of height H, total mass m, and that the center of gravity (CoG) is situated along the middle, at a height n×H where n is a coefficient (0<n<1). This allows us to transfer the problem to a single dimension (z').
This is equivalent to the following situation, where ρ1 and ρ2 represent the equivalent density aft and fore of the CoG.

By definition:
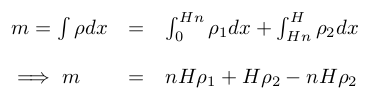
And, from the position of the CoG, we have:
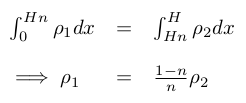
Hence:
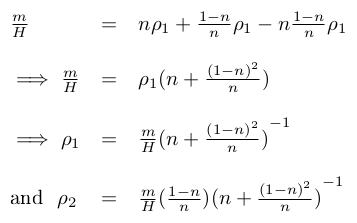
From this point, we can compute I:
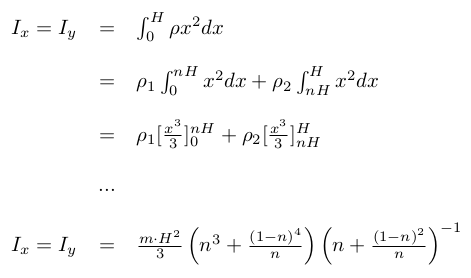
Finally, similarly to translation, these equations must be discretized:
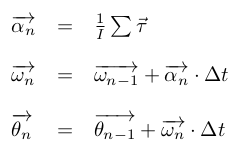
Code
Impulse is developped in Java, making it both efficient and cross-platform. All of its code is released under MIT license.
The source code is very modular, with extensive usage of the object-oriented design principles. Therefore, it is very expendable: more motor types (hybrid, liquid fuel), multi-staging, etc. Every class is fully commented using standard Javadoc format.
Special thanks to Alexey Sokolov (JSSC), Ralf Sternberg (minimal-json) and Konstantin Bulenkov (DarculaLaf) for their great open-source libraries!
Limitations
There are still limitations to this simulator:
- It does not simulate aerodynamic drag. I advise using the great OpenRocket software for accurate, open-source simulation of those forces.
- Currently, one degree of freedom is completely absent: the rotation around the vertical axis of the rocket. Although it is not required in my physics model, it might be added in the future.
- It makes several reasonable assumptions:
- The rocket's mass repartition is radially symmetrical;
- The rocket's mass doesn't change throughout the flight (yet).
In the future, I plan to:
- Priority: implement simulation of aerodynamic forces. This is quite a bit harder than in most other simulators because of the assumptions I can't make, due to the absence of fins!
- Import a complete motor database to provide the most often used thrust curves.
- Create an Arduino library to make the usage of Impulse with Arduino much easier.
Author: Charles Grassin
What is on your mind?
Sorry, comments are temporarily disabled.
#1 Boris
on February 27 2020, 8:17